Srinivasa Ramanujan: The Man Who Knew Infinity!

Srinivasa Ramanujan Ji (श्रीनिवास रामानुजन जी) (1887–1920) is a name that stands synonymous with raw brilliance and mathematical genius. Despite a short life filled with struggles and hardships, he carved his name into the annals of history with groundbreaking contributions that continue to astonish mathematicians today. His journey from a modest upbringing in India to being celebrated as one of the most remarkable mathematical minds ever is nothing short of awe-inspiring.

In this article, we delve deeper into the life, works, struggles, and enduring legacy of Srinivasa Ramanujan—a man whose intuitive grasp of mathematics transcended the limitations of formal education.

Early Life: A Prodigy from Erode!

Srinivasa Ramanujan (श्रीनिवास रामानुजन) was born on December 22, 1887, in Erode, Tamil Nadu, in a Brahmin family (ब्राह्मण परिवार). His father, K. Srinivasa Iyengar (के. श्रीनिवास अयंगर), was a clerk, and his mother, Komalatammal (कोमलातम्मल), was a devout homemaker and temple singer. When Ramanujan was just a year old, the family moved to Kumbakonam, a small town steeped in religious and cultural traditions.

From an early age, Ramanujan displayed an extraordinary aptitude for mathematics. By the age of 10, he had mastered advanced arithmetic and trigonometry, often solving complex problems without any formal guidance. His teachers were astonished at his ability to derive solutions in unconventional ways, often bypassing established methods.

However, his life took a pivotal turn at the age of 15 when he encountered G.S. Carr’s book "A Synopsis of Elementary Results in Pure and Applied Mathematics." This book was a compilation of 6,000 mathematical results, presented without proofs. Ramanujan devoured its contents, deriving proofs for the results and using the book as a springboard for his own independent discoveries.

The Lonely Pursuit of Mathematics!

• Despite his mathematical brilliance, Ramanujan faced significant challenges in his academic journey. His single-minded focus on mathematics caused him to neglect other subjects, leading to poor academic performance. He failed his college exams multiple times, which cost him the opportunity to obtain a formal degree.

• This period of his life was marked by isolation, poverty, and rejection. Yet Ramanujan continued to immerse himself in mathematics, filling notebooks with his discoveries. These notebooks, later known as the "Ramanujan Notebooks," contained thousands of theorems, many of which were far ahead of their time.

• In 1909, he married Janaki Ammal (जानकी अम्मल), and the financial pressures of supporting a family forced him to seek employment. He found work as a clerk at the Madras Port Trust in 1912. Here, his mathematical talents came to the attention of his supervisor, who recognized his potential and encouraged him to reach out to mathematicians abroad.

The Turning Point: Connecting with G.H. Hardy!

In 1913, Ramanujan wrote a now-famous letter to G.H. Hardy, a prominent mathematician at Cambridge University. The letter contained over 100 mathematical theorems, many of which were entirely novel. Hardy, initially skeptical, recognized the extraordinary originality of Ramanujan’s work.

Hardy later described his first impression of Ramanujan as one of amazement:
"I had never seen anything in the least like them before. A single look at them is enough to show that they could only be written down by a mathematician of the highest class. They must be true, because if they were not true, no one would have had the imagination to invent them."

Hardy, along with fellow mathematician J.E. Littlewood, arranged for Ramanujan to come to England. In 1914, after much deliberation, Ramanujan made the arduous journey to Cambridge—a decision that marked the beginning of his most productive years.

The Cambridge Years: Unleashing Genius

At Cambridge, the collaboration between Ramanujan and Hardy became one of the most celebrated partnerships in mathematical history. While Hardy provided the rigorous academic framework that Ramanujan lacked, Ramanujan brought an unparalleled level of creativity and intuition to their work.

During his time at Cambridge, Ramanujan made significant contributions to several fields, including

• Number Theory: His work on prime numbers, particularly the discovery of the Ramanujan prime, remains fundamental to this day.

• Partition Theory: Ramanujan and Hardy developed the Hardy-Ramanujan asymptotic formula, which provides an approximation for the partition function, a critical concept in combinatorics.

• Modular Forms: His research on modular forms and the Ramanujan theta function laid the groundwork for later developments in string theory and quantum physics.

• Infinite Series: Ramanujan’s work on infinite series, including the astonishing Ramanujan Summation, continues to intrigue mathematicians.

Ramanujan’s ability to intuitively derive results, often bypassing traditional methods, left even the most seasoned mathematicians baffled. He often attributed his insights to divine inspiration, claiming that the Hindu goddess Namagiri revealed mathematical truths to him in his dreams.

Ramanujan’s Intuitive Genius

One of the most remarkable aspects of Ramanujan’s work was his intuition. He often derived equations and theorems without formal proof, relying on a deep sense of numbers and relationships that seemed almost mystical. While this initially perplexed mathematicians, later studies validated the vast majority of his findings, proving their correctness.

Ramanujan’s insights were frequently so advanced that contemporary mathematicians struggled to comprehend their depth. His enigmatic methods prompted G.H. Hardy to rank him among the greatest mathematicians in history, alongside names like Euler, Gauss, and Newton.

Hardy once described his collaboration with Ramanujan, saying:
"I have never met his equal, and I can compare him only with Euler or Jacobi."

Contributions to Advanced Mathematics

Mock Theta Functions

• Ramanujan’s final letter to Hardy, written on his deathbed, introduced the concept of "mock theta functions." These functions are now recognized as fundamental in areas such as number theory, modular forms, and mathematical physics.

Tau Function and Ramanujan Conjecture

• Ramanujan conjectured properties of the tau function, which were later proven using modern mathematical techniques. His conjectures laid the groundwork for significant developments in algebraic geometry and representation theory.

Partition Functions

• Ramanujan’s work on partition numbers revolutionized combinatorics. His insights into the partition function led to a deep understanding of how integers can be expressed as sums, with implications for cryptography and computational mathematics.

Ramanujan-Hardy Number (1729)

• The number 1729, famously known as the Hardy-Ramanujan number, is the smallest positive integer that can be expressed as the sum of two cubes in two distinct ways:

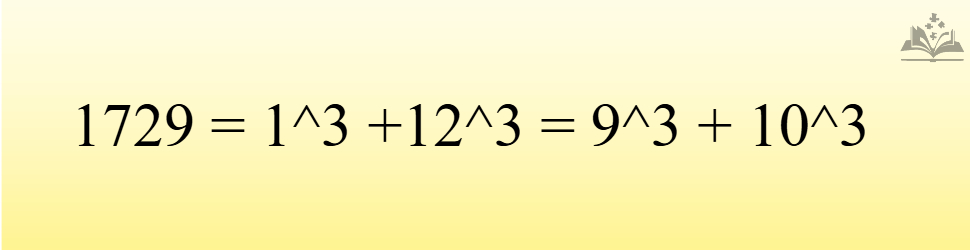
This anecdote, shared by Hardy, reflects Ramanujan’s extraordinary ability to identify mathematical patterns in seemingly ordinary numbers.

Cultural and Religious Influences

Ramanujan Ji’s life and work were deeply influenced by his Hindu faith and devotion. He often credited his mathematical discoveries to the blessings of the Maa Namagiri (माँ नामगिरि), whom he regarded as his spiritual guide. His intuitive methods and belief in divine inspiration reveal a unique blend of faith and intellect, illustrating the role of culture in shaping his genius.

His notebooks often included references to traditional Indian mathematics, showing how his work was rooted in both indigenous knowledge systems and modern mathematics.

The Mysteries of His Notebooks

Ramanujan left behind three notebooks and a "lost notebook," discovered posthumously, containing thousands of formulas and theorems. Mathematicians have spent decades deciphering these works, uncovering new mathematical truths and applications.

Even today, researchers describe these notebooks as treasure troves of unsolved problems and cutting-edge mathematics. Ramanujan’s ability to think far ahead of his time continues to influence research in areas such as

• String theory

• Statistical mechanics

• Quantum field theory

Impact on Modern Science and Technology

Ramanujan Ji’s contributions extend beyond pure mathematics into practical applications in modern science and technology. His formulas are used in:

• Cryptography: Partition functions and modular forms play a key role in secure digital communications.

• Physics: His work on infinite series and modular forms is applied to understanding black holes and quantum mechanics.

• Computer Algorithms: Ramanujan’s insights into number theory and approximation methods are foundational in developing algorithms for high-performance computing.

Personal Challenges and Resilience

Despite his extraordinary talent, Ramanujan faced immense personal and professional challenges. These include:

• Financial Hardship: He struggled with poverty throughout his life, especially during his early years in India.

• Health Issues: Years of malnutrition and illness ultimately cut his life short, depriving the world of further groundbreaking contributions.

• Cultural Alienation: His time in England was marked by cultural and social isolation, compounded by dietary restrictions as a practicing Hindu.

Yet Ramanujan’s unwavering passion for mathematics allowed him to persevere. His resilience in the face of adversity is a testament to his indomitable spirit.

Inspirational Legacy

Ramanujan’s life story resonates with anyone who faces obstacles in pursuing their passions. His journey from a small town in Tamil Nadu to global recognition proves that genius can emerge from the most unlikely circumstances.

In his honor

• UNESCO declared 2012 the "Year of Mathematics" to celebrate his 125th birth anniversary.

• The Ramanujan Prize was established to recognize outstanding mathematicians from developing countries.

His life has inspired books, documentaries, and films, most notably the biographical drama "The Man Who Knew Infinity," which brought his story to a global audience.

Ramanujan in the Context of Global Mathematics

Ramanujan’s story transcends national boundaries. His intuitive style, coupled with the formal rigor imposed by Hardy, represents a confluence of Eastern and Western approaches to mathematics. This unique synthesis underscores the universality of mathematical thought and its power to unite diverse cultures.

Health Decline and Tragic End

The years Ramanujan spent in England were both intellectually rewarding and physically taxing. The cold climate, cultural isolation, and dietary restrictions took a toll on his health. In 1917, he was diagnosed with severe health issues, including tuberculosis and vitamin deficiencies.

Despite his deteriorating health, Ramanujan continued to work tirelessly. In 1918, he became the first Indian to be elected a Fellow of the Royal Society, one of the highest honors in the scientific community. He was also elected a Fellow of Trinity College, Cambridge.

In 1919, a gravely ill Ramanujan returned to India. He spent his final months in Kumbakonam, continuing to work on mathematics from his deathbed. He passed away on April 26, 1920, at the age of 32, leaving behind a legacy that would inspire generations to come.

The Legacy of a Genius

Ramanujan’s contributions to mathematics are immeasurable. His notebooks, containing over 3,900 results, continue to be studied and yield new discoveries even a century after his death. Key aspects of his legacy include:

• Mathematical Influence: His work has applications in physics, computer science, and cryptography, particularly in the study of black holes and string theory.

• Posthumous Recognition: In 1987, the Ramanujan Journal was established to publish research inspired by his work. His contributions were also celebrated in the 2015 biographical film "The Man Who Knew Infinity."

• Inspiration: Ramanujan’s story has inspired countless individuals to pursue mathematics, proving that genius can emerge from the most unlikely circumstances.

Honors and Commemorations

Srinivasa Ramanujan has been widely honored both in India and internationally.

• December 22, his birthday, is celebrated as National Mathematics Day in India.

• The Ramanujan Institute for Advanced Study in Mathematics in Chennai is named in his honor.

• In 2012, NASA named a supercomputer "Ramanujan" to recognize his contributions to mathematics.

• The Government of India released a commemorative stamp in his memory.

Srinivasa Ramanujan Ji’s brilliance is a reminder of the untapped potential within every individual. His legacy continues to inspire mathematicians, scientists, and dreamers worldwide. Despite living only 32 years, Ramanujan left an indelible mark on the world—a mark that will endure for generations.

His extraordinary ability to see beauty in numbers, coupled with his perseverance against all odds, ensures that his contributions to mathematics and humanity will never be forgotten. As G.H. Hardy aptly said, “The world has a right to know more about Ramanujan.”

Let us celebrate this genius not just for his remarkable achievements but also for his unwavering dedication to the pursuit of knowledge.

Support Us by buying coffee.❤️❤️